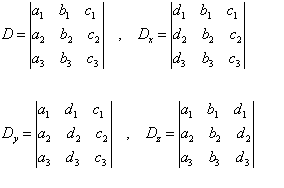Cramer's Rule

Given a system of linear equations, Cramer's Rule is a handy way to solve for just one of the variables without having to solve the whole system of equations. They don't usually teach Cramer's Rule this way, but this is supposed to be the point of the Rule: instead of solving the entire system of equations, you can use Cramer's to solve for just one single variable. 

Let's use the following system of equations: 

2x + y + z = 3 

x – y – z = 0 

x + 2y + z = 0

We have the left-hand side of the system with the variables (the "coefficient matrix") and the right-hand side with the answer values. Let D be the determinant of the coefficient matrix of the above system, and let Dx be the determinant formed by replacing the x-column values with the answer-column values:

Systems of Equations 

A system of equations is a set or collection of equations that you deal with all together at once. Linear equations (ones that graph as straight lines) are simpler than non-linear equations, and the simplest linear system is one with two equations and two variables. Think back to linear equations. For instance, consider the linear equation y = 3x – 5. A "solution" to this equation was any x, y-point that "worked" in the equation. 

So (2, 1) was a solution because, plugging in 2 for x: 

3x – 5 = 3(2) – 5 = 6 – 5 = 1 = y 

On the other hand, (1, 2) was not a solution, because, plugging in 1 for x: 

 3x – 5 = 3(1) – 5 = 3 – 5 = –2

Since the two equations above are in a system, we deal with them together at the same time. In particular, we can graph them together on the same axis system.

A solution for a single equation is any point that lies on the line for that equation. A solution for a system of equations is any point that lies on each line in the system. For example, the red point at right is not a solution to the system, because it is not on either line.

Graphing Polar Equations

The most basic method of graphing polar equations is by plotting points and doing a quick sketch. Graphing polar equations is a skill that requires the ability to plot points and sometimes recognize a special case of polar curves, such as cardioids, and roses and conic sections. However, we need to understand the polar coordinate system and how to plot points for graphing polar equations. The graph of a polar equation r = f(θ), or more generally F(r, θ) = 0, consists of all points P that have at least one polar representation (r, θ) whose coordinates satisfy the equation. EXAMPLE: Sketch the polar curve θ = 1. Solution: This curve consists of all points (r, θ) such that the polar angle θ is 1 radian. It is the straight line that passes through O and makes an angle of 1 radian with the polar axis. Notice that the points (r, 1) on the line with r > 0 are in the first quadrant, whereas those with r < 0 are in the third quadrant.
And these are the polar equations that I had created.

Polar Coordinates

The polar coordinates r (the radial coordinate) and theta (the angular coordinate, often called the polar angle) are defined in terms of Cartesian coordinates by:

 x = rcostheta (1) y = rsintheta

where r is the radial distance from the origin, and theta is the counterclockwise angle from the x-axis. In terms of √(x^2+y^2) (3) theta = tan^(-1)(y/x). (4) (Here, tan^(-1)(y/x) should be interpreted as the two-argument inverse tangent which takes the signs of x and y into account to determine in which quadrant theta lies.) It follows immediately that polar coordinates aren't inherently unique; in particular, (r,theta+2npi) will be precisely the same polar point as (r,theta) for any integer n. What's more, one often allows negative values of r under the assumption that (-r,theta) is plotted identically to (r,theta+/-pi).

We start with a cartesian coordinate system. We choose O as pole and the x-axis as polar-axis. The cartesian coordinates of a point P are (x,y). Choose the u-axis such that r > 0. then P = r U => P2 = r2 U2 => x2 + y2 = r2 r = sqrt(x2 + y2) Now, choose a t-value such that x = r.cos t and y = r.sin t