Systems of Equations 

A system of equations is a set or collection of equations that you deal with all together at once. Linear equations (ones that graph as straight lines) are simpler than non-linear equations, and the simplest linear system is one with two equations and two variables. Think back to linear equations. For instance, consider the linear equation y = 3x – 5. A "solution" to this equation was any x, y-point that "worked" in the equation. 

So (2, 1) was a solution because, plugging in 2 for x: 

3x – 5 = 3(2) – 5 = 6 – 5 = 1 = y 

On the other hand, (1, 2) was not a solution, because, plugging in 1 for x: 

 3x – 5 = 3(1) – 5 = 3 – 5 = –2

Since the two equations above are in a system, we deal with them together at the same time. In particular, we can graph them together on the same axis system.

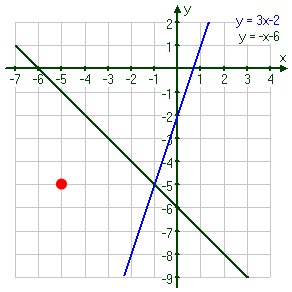
A solution for a single equation is any point that lies on the line for that equation. A solution for a system of equations is any point that lies on each line in the system. For example, the red point at right is not a solution to the system, because it is not on either line.